Importance Sampling
[[Monte Carlo]],[[近似求定积分]]
f(x) 在 [a,b] 上的积分很难直接求,利用采样的方法进行计算。
$\int_{a}^{b} f(x) d x=\frac{b-a}{N} \sum_{i=1}^{N} f\left(x_{i}\right)$
假设需要估计期望 $E_{x \sim p}[f(x)]$,$p$ 表示采样变量 $x$ 的分布
$E_{x^{\sim} p}[f(x)]$ :-> $\int p(x) f(x) d x \approx \frac{1}{N} \sum_{i=1}^N f\left(x_i\right)$
- 如果分布 $p$ 很难积分 :-> 通过 $p$ 采样来进行期望的估计
- 如果 $p$ 采样很麻烦 :-> 用更简单的已知分布 $q$ 来代为采样
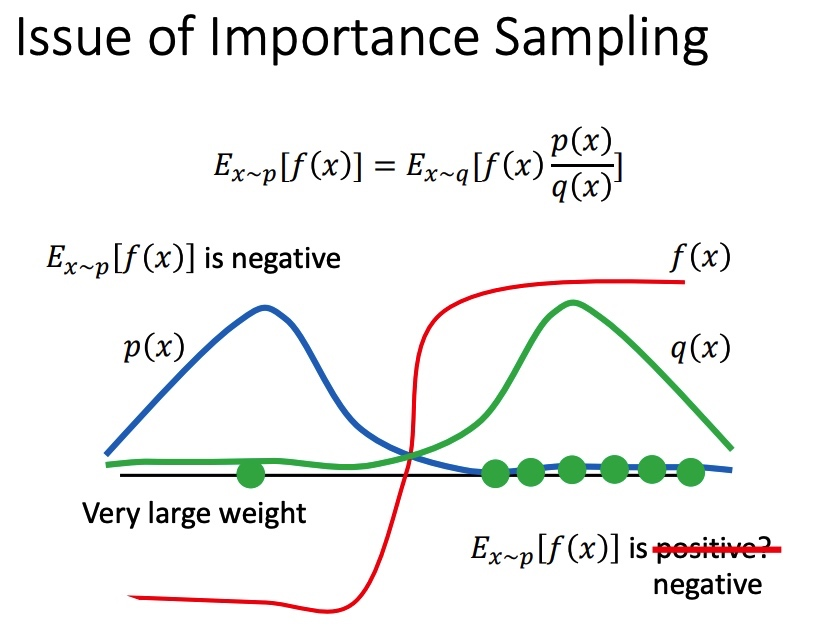
在 $q$ 分布下计算期望公式 :-> $E_{x^{\sim} p}[f(x)]=E_{x^{\sim} q}[\frac{p(x)}{q(x)}f(x)]$
重要性采样对估计的 [[方差与均值]] 影响 :-> 均值一致,但方差并不能确定一致已知期望计算方差公式 :-> $\operatorname{Var}(x)=E\left(x^2\right)-[E(x)]^2$
原分布p方差定义为 :-> $\operatorname{Var}{x^{\sim}p}[f(x)]=E{x^{\sim}p}\left[f(x)^{2}\right]-\left(E_{x^{\sim}p}[f(x)]\right)^{2}$
新分布q方差 :-> ${\operatorname{Var}{x \sim q}\left[f(x) \frac{p(x)}{q(x)}\right]=E{x \sim q}\left[\left(f(x) \frac{p(x)}{q(x)}\right)^{2}\right]-\left(E_{x \sim q}\left[f(x) \frac{p(x)}{q(x)}\right]\right)^{2}}$
- 最终方差 :-> $\operatorname{Var}{x^{\sim} q}\left[\frac{p(x)}{q(x)} f(x)\right]=E{x^{\sim} p}\left[\frac{p(x)}{q(x)} f(x)^2\right]-\left(E_{x^{\sim} p}[f(x)]\right)^2$
- 如何推导出最终方差 #card
- $E_{x^{\sim} q}\left[\left(\frac{p(x)}{q(x)} f(x)\right)^2\right]=\int\left(\frac{p(x)}{q(x)} f(x)\right)^2 q(x) d x=\int \frac{p(x)}{q(x)} f(x)^2 p(x) d x=E_{x^{\sim} p}\left[\frac{p(x)}{q(x)} f(x)^2\right]$
- $\left(E_{x^{\sim} q}\left[\frac{p(x)}{q(x)} f(x)\right]\right)^2=\left(E_{x^{\sim} p}[f(x)]\right)^2$
- 如何推导出最终方差 #card
- 最终方差 :-> $\operatorname{Var}{x^{\sim} q}\left[\frac{p(x)}{q(x)} f(x)\right]=E{x^{\sim} p}\left[\frac{p(x)}{q(x)} f(x)^2\right]-\left(E_{x^{\sim} p}[f(x)]\right)^2$
根据 原分布p方差定义为 :-> $\operatorname{Var}{x^{\sim}p}[f(x)]=E{x^{\sim}p}\left[f(x)^{2}\right]-\left(E_{x^{\sim}p}[f(x)]\right)^{2}$
和 ((66dc826d-6ba6-4a23-bf77-ce297d3e25d3))- 当分布 p、q 越接近, 其方差就越接近 ,而如果两者差距很大时, 则方差差别很大
- [[Importance Weight]] :<-> $\frac{p(x)}{q(x)}$
- 在采样次数较少时,基于重要性采样得到的样本并不能 很好反映变量的原始分布 ,从而产生较大误差。
[[Ref]]
[[李宏毅@强化学习]]
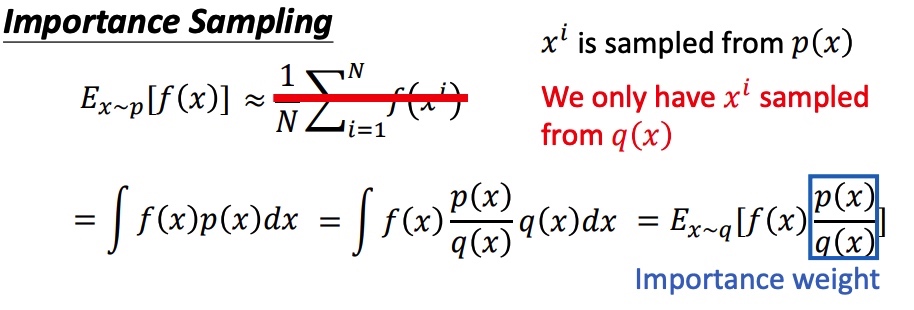
[[PPO]] 中实现
在每次策略更新之前,使用旧策略采集的一批轨迹数据。
对于每个轨迹数据点,计算新策略在旧策略下的采样概率比率,即重要性采样比率。比率的计算可以根据具体的策略表示形式进行推导。
根据重要性采样比率,对采样的数据点计算重要性采样权重,用于校正策略梯度的估计。权重的计算通常是将比率取倒数,并进行归一化处理。
使用校正后的重要性采样权重来计算策略梯度,并进行策略更新。
[[PPO 基本训练流程]]
Importance Sampling
https://blog.xiang578.com/post/logseq/Importance Sampling.html